Entangled Identity of Quantum Indiscernibles
All fundamental particles in nature are, as far as we can tell, identical to one another. Two photons, the particles of light, could have the same frequency, the same polarization and could travel in the same direction, i.e. all of their features could in principle be identical. Some philosophers, in this case Leibniz first and foremost, would then call into question the fact that we choose to talk about two photons. In other words, if they are identical in all their aspects how can we discriminate them to even say that there are two such entities? Descartes would have answered (I am being a bit anachronistic here as Descartes lived before Leibniz) that there is one property that could still be used for discrimination and this is their position, one photon could be here and the other one over there.
This seems like a good piece of logic, but what if the two photons even happened to occupy the same spatial location? The interesting thing then is that we would still have two photons, but we would never be able to tell which one is which (my feeling is that Leibniz would have got this one wrong, insisting that – in such a case – there is really only one photon; this is what he meant by the “principle of the identity of indiscernible”).
And this has spectacular consequences in physics. It brings me to one of the most beautiful experiments ever, which goes under the name of Hong-Ou-Mandel. Unless you are a quantum optician, chances are you’ve never heard of this experiment even if you are a practicing physicist! And that’s a shame since the Hong-Ou-Mandel logic plays out in almost all domains of physics where quantum mechanics plays a role (I will give you an example from high energy physics later on but I could equally well choose solid state physics or anything else, wherever quantum physics matters).
Hong, Ou and Mandel used photons to study the quantum indistinguishability of identical particles, in their case also photons. When two photons interact (at a beamsplitter) and one comes in through one port and the other through the other port, if they are in the same physical state (the same frequency and polarization), they will always bunch. That means that, at the output of the beamsplittter, both photons will go one way or the other, but never separately.
What if the photons are in different states, say one is polarized horizontally (H) and the other one vertically (V)? Then they are distinguishable and therefore go all possible ways (namely, there is also the possibility that one photon goes one way and the other one the other way and there are two such possibilities since H can go to the left and V to the right and vice versa).
But, and here is where the Hong-Ou-Mandel ingenuity comes to the fore, what happens if the two photons are created with different polarizations, but just before they are about to interact at the beamsplitter, we change their polarizations to make them the same? In other words, will the fact that they are distinguishable for most of their existence count when they interact, if at the point of interaction they are the same? The answer is NO! They now interact as completely indistinguishable particles would and bunch, meaning that they leave the beamsplitter in the same direction. So what matters is whether, when they occupy the same spatial location, they also have all the other properties the same.
Hong-Ou-Mandel also tested the third possible scenario, which is to start the photons in the same state, but then, last minute, just before they reach the beamsplitter, they change the polarizations to make them different. Then, as you would have guessed by now, they scatter just as perfectly distinguishable particles would.
Is there another way to make the photons distinguishable? Yes. They could arrive at the beamsplitter at different times so that their spatial states do not overlap at all. Then they also behave as distinguishable particles since they go through the beamsplitter completely independently, one after the other.
So far, we discussed particles that bunch when they are indistinguishable, and these are called bosons. We have another kind of particle, which tends to do the opposite (anti-bunch) when indistinguishable. Electrons are such particles, and the Hong-Ou-Mandel type experiments with electrons would give the opposite results to photons (namely, they would anti-bunch, i.e. go their separate ways when indistinguishable, and would display all possible behaviours when in different states and therefore distinguishable).
Given that most of physics is to do with the interactions between photons and electrons, the behaviour of the above kind is ubiquitous in nature. The fact that fermions anti-bunch leads to matter being hard and stable (the famous Pauli Exclusion Principle). Bosons, on the other hand, provide forces that lead to coupling between different parts of matter. This forms the basis for our deepest understanding of the universe.
But I would now like to tell you something I found amazing. I want to discuss a recent experiment that comes from particle physics and is underpinned by the Hong-Ou-Mandel logic. It’s from the STAR collaboration at the Relativistic Hadron Collider, Brookhaven National Laboratory.
I only became aware of this latest of their experiments because someone asked me to comment on it on the radio (which I didn’t do because, since you asked, it was a morning program taking place too early for me to wake up for). Anyway, I did read their paper as it contained some claims about entanglement, which is – as most of you will know – my favourite topic in physics.
So what did the STAR team do? They smashed two heavy atomic nuclei into one another at high speeds. This produced photons, which then interacted with the nuclei triggering production of rho mesons (these are the excited states of the pi mesons) and these then finally decayed into a pi+ and a pi- meson (there is a zoo of particles at high energies and I might dedicate a later blog to telling you about this part of physics in more depth). These positively and negatively charged pions are the particles that are ultimately detected.
Since there are two nuclei and each undergoes the same cascade, we finally have two pairs of pions. In what follows, it will be helpful to think of the two kinds of pions (the positive and the negative) being exactly like the two differently polarized photons. The photon polarization is analogous to the pion charge, and it is the degree of freedom we can use to discriminate between the pions (which are otherwise the same – they have the same mass and spin, which are their other defining features in addition to charge).
From the interference fringes, which represents the pion detector clicks as a function of the angle, the STAR team concludes that the pion pairs must be entangled. This means that the states that we get from the decay of the rho meson are of the entangled form,|p+,p-> + |p-,p+>, and there are two such states in total.
The amazing thing for me was that the phenomenon encountered here is the same as what I analysed some twenty odd years ago with my colleagues from Oxford. The idea is to actually use the bosonic indistinguishability to transfer entanglement from the internal to the spatial degrees of freedom of photons. In my paper, two pairs of photons were entangled in polarization, but after interaction, they become entangled spatially (so that if two photons go one way, the other two go in the opposite direction). Figure below will give you the set-up, but the mathematics is virtually the same as in the pion experiment!
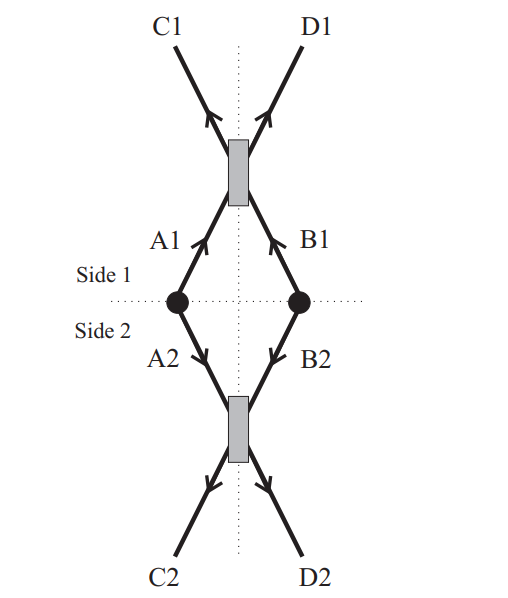
The two pairs of photons A1 and A2 and B1 and B2 are entangled in the internal degrees of freedom. As A1 interacts with B1 at a beamsplitter and A2 with B2 at another beamsplitter, the state at the output modes C and D becomes spatially entangled. So, for instance, if we get two photons bunching in C1, then there will be two photons in C2 as well. Therefore, the initial internal entanglement is converted into the spatial entanglement between sides 1 and 2.
This is of course the beauty of physics, its greater and greater unification of more and more disparate phenomena, under the umbrella of a very small number of (in this case quantum) principles. Ultimately, as Schrödinger taught us a lot time ago, it is really all about entanglement. And, something that he would possibly not have considered as fundamental, but was crucial for the experiments here, was the identity of quantum indiscernibles.
Sign up to my substack if you'd like to have my articles delivered straight to your inbox
ASK ME ANYTHING!
If you'd like to ask me a question or discuss my research then please get in touch.





