Imaginary time, Twin Paradox and Bell’s Inequalities

The interesting thing about imaginary numbers, like the square root of -1, is that it took two major revolutions in physics to actually make them real. Those of you who read some of my previous blogs on the relationship between mathematics and physics, will know that I hold physics in higher regard ☺, though, of course, it is worth remembering Galileo, who said that the book of nature is written in the language of mathematics.

Anyway, back to imaginary numbers. Some other Italian Renaissance guy called Cardano (himself also a polymath, like most renaissance thinkers) introduced imaginary numbers to solve cubic equations. He probably thought of them as just a clever mathematical device and nothing more than that (the very name “imaginary” suggests that they are not as real as the real numbers). Everyone else thought the same and the imaginary numbers continued to have this inferior reputation for about 400 years. The discovery of special relativity changed all that.

One way to think about relativity is that its whole point is to upgrade time to a fourth dimension (in addition to the three spatial ones) but with a twist. It is the imaginary “i times time t”, that becomes the fourth dimension. Time, in other words, could be seen as the imaginary fourth component of spacetime.

For anything that happens in the universe, relativity assigns to it four coordinates – three spatial ones telling us “where” it happened, and one temporal one telling us “when” it happened. Minkowski was the first person to think of relativity this way (ironically, the idea was initially not appreciated even by the originator of the theory of relativity, Einstein, who called Minkowski’s construct a “mental masturbation”).

The distance between two events is now measured in this four dimensional spacetime and, because time is imaginary, this distance becomes equal to x^2+y^2+z^2+(it)^2 = x^2+y^2+z^2-t^2. In other words, there is a minus sign in front of t^2 (Some of you may have realized that t should be multiplied by the speed of light c, but in the best tradition of theoretical physics, I am assuming that c=1).

This is interesting, because this kind of a distance is not really a distance! Namely, it is not true that AB+BC>=AC. This inequality is known as the triangle inequality (for obvious reasons, see the picture) and it is violated in relativity. In other words, going directly from A to C, could – in relativity – take longer than going via another point B.

The extreme example of this is when light goes from A to B and from B to C so that C ends up in the same spatial location as A (imagine a flash of light generated at A, then travelling to a mirror at B and bouncing back to return to A at a later time, which is the point C in spacetime). Then both AB and BC are zero (the paths that light takes are thus called null rays), while AC is some finite interval of time (whatever it took light to make the round trip from A to B and back). The longest way round is, as far as relativity is concerned, the shortest way home.

From the fact that AC>AB+BC all sorts of weird relativistic results follow. For instance, take the famous twin paradox. The twin that travels away and comes back ends up being younger, at the end of the journey, than his stationary brother. The stationary brother ages by AC which, as we saw, is greater than AB plus BC, which corresponds to the ageing of the traveling twin.

We know that twins cannot travel at the speed of light, but the same is true for any speed of travel, it is just that the difference between the ages gets smaller (this is a shame because, if we could travel at the speed of light we would not age at all!).

If some people still had reservations about the reality of imaginary numbers after Minkowski then quantum physics (which came some 20 years later) finally clinched the issue. The key equation in quantum physics, the Schrödinger equation, is actually a diffusion equation, but the diffusion of a particles that it describes actually takes place in the imaginary time. The square root of minus one is simply unavoidable in quantum physics. This has all sorts of interesting consequences, such as the fact that, unlike the diffusion equation, the Schrödinger equation is fully reversible. Matter wave interference is all about this, namely the fact that material objects also behave like waves.

But, does the presence of the imaginary numbers also mean that quantum physics violates the triangle inequality? The answer is yes and this violation is known as Bell’s inequalities!

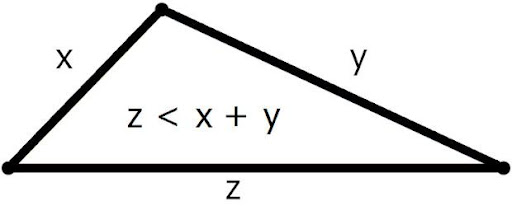
Triangle inequality says that the sum of any two sides of a triangle is always greater than the third side. Not so in theory of relativity (e.g. the twin paradox) and quantum physics (e.g. Bell’s inequalities).

In quantum mechanics the points A, B and C represent measurements on quantum systems instead of points in spacetime. We can make measurements on a quantum system so close to one another – meaning that the basis in which the measurements are made are almost, but not quite, the same – so that their outcomes are almost identical. In other words, the distance between these measurements, in the sense of the proximity of the outcomes, will, to the lowest order of approximation, be zero.

Imagine now that we do a sequence of such very close measurements, A is close to B, B is close to C and so on. If we keep going like this, we will end up with a measurement, call it Z, which is very different to A, so that the distance between them is equal to 1 (i.e. maximal). In other words, we add up lots of zeroes to get a distance equal to one. The inequality AB+BC+…>=AZ is thus violated (0>=1). For those who are interested in learning more, please have a look at the recent experiments I was involved with https://www.science.org/doi/full/10.1126/sciadv.abe4742.

I’ve described measurements on one particle, but if you perform this on two entangled particles, so that the measurements alternate between the two), you will obtain the Bell inequalities (and, incidentally, the inequality on one particle is sometimes called the Leggett-Garg inequality).

Finally, at the risk of completely spoiling the coherence of the above narrative, I will offer two words to caution. In general relativity it is no longer fruitful to think of time as imaginary. This is because the distance measure now might also contain products of space and time (terms like dx dt) and thinking of time as imaginary here doesn’t really do us much good. Secondly, the violation of Bell’s inequality could also be true in what some people call “real quantum mechanics”, which entails using only real numbers as amplitudes. However, real quantum mechanics is insufficient to account for even some basic interference experiments and, more importantly, the “i” in the Schrödinger equation is still there when accounting for dynamical evolution between different measurement bases.