An Unbroken Thread of Discovery

Clearly all of these Medieval physicists (they call them “mathematicians” or “philosophers” because physics did not exist back then as a science – it only established itself properly as a separate discipline with Galileo and Newton in the seventeenth century) were influenced by Euclid and tried to expose everything in the format of “theorems and proofs”. However, most of these proofs look more like desperate struggles to justify, by hook or by crook, the intuitively preformed conclusions (nothing wrong with the latter, of course, that’s how the conjectures are made). They remind me of some exam scripts of my students when they clearly don’t know how to solve the problem they are asked to solve, and they then write down all they can think of related to the subject at hand, hoping to get some extra marks…(again, nothing wrong with that strategy, we all do it, but it just doesn’t constitute a mathematically valid proof).

However, the thing that strikes you the most as you browse though this wonderful collection, is how slow and gradual the whole process of discovery has been. One feels like a palaeontologist must feel when they look at a long chain of fossil records noting all the tiny evolutionary changes that take an inordinate amount of geological time to complete. Sometimes these mutations go “backwards”, away from the “desired” end, making frequently one step forward and then a couple of steps backward. Basically, the whole of Medieval mechanics was about trying to understand the concept of motion and it took them more than 10 centuries (excluding the prior 10 when the Greeks worked on it too!) to arrive at, what one might call, a single crowning achievement.

I will tell you about that crowning achievement in a minute, but let me just say that this is not the impression we get of the scientific progress when we learn physics in high school. We learn about Newton’s laws in more or less a handful of lessons and are then expected to be able to apply them to various situations in the subsequent classes. It takes about a year or two to fully master classical mechanics (while studying other subject too!), but as we do that, we are not made to be aware of how long and laborious the whole process of discovery has actually been to arrive at something like Newton’s laws of motion.

Granted, Newton was a genius, but it seems to me that our educational system gives us the impression that he was a miracle worker and did the near impossible. That he made leaps from nowhere and gave us these beautiful and complete laws just by thinking about things. Nothing could be further from the truth. Newton was definitely familiar with all the key medieval (and ancient) literature, and he also knew one important result that is mistakenly attributed to Galileo and which I called the crowning achievement of the medieval mechanics.

Newton was of course the first to acknowledge standing on the shoulders of giants. His contribution can be seen more as part of a continuous effort stretching over a couple of millennia or so. Almost all the key ideas have been tried before him and each had a varying degree of success, with things clearly improving overall with time, but in a slow and gradual and haphazard fashion. History of physics is a bit like that joke with Einstein standing in front of a blackboard and trying out the formula E=ma2, then crossing it out, then trying out E=mb2, then again crossing it out, only to finally arrive at the correct E=mc2. This is obviously not how he did it (at least I hope not), but, like all good jokes, there is a great deal of truth in it.

The evolution of science is an unbroken threat of ideas, the later slightly tweaking and building on the previous ones, much like the evolutionary equivalent of the unbroken thread of life starting with a single living system and evolving into what we now see around us. And, of course, even classical mechanics didn’t stop evolving with Newton (just like life didn’t stop after producing monkeys), it continued to be modified by Lagrange, Hamilton and many many others. I’ve written before about how important in particular that last step of Hamilton’s was for quantum physics.

Now, the crowning achievement. It is a result attributed to the so-called Merton calculators. These were 14th century mathematicians (remember, physics did not exist back then) based at Merton College in Oxford, who proved (one of them proved it, I believe, – you can look it up as the Wiki will certainly know it better than me) what is known as the mean velocity theorem.

Here is what the theorem says. If a body starts from rest and accelerates uniformly (as in Earth’s gravity, which is why they were interested in this, and also why Newton knew about it) then the distance it travels equals the product of half its final speed times the time of travel. So as a body accelerates uniformly from zero to its final velocity, the distance its travelled during this time is the same as if it were to move at a constant velocity provided that that velocity was half the final velocity. If the body already starts in motion, then we need to take the sum of the initial and the final velocities divided by two (hence the name “mean velocity theorem”).

This is really just another way of saying that the distance travelled is one half the acceleration times the time squared (a formula we all learn in high school, s=at2/2). The way that the Merton calculators proved this was really interesting. This is the proof we mistakenly credit to Galileo – I certainly did, and it is entirely geometrical in nature (again in the good old style of Euclid).

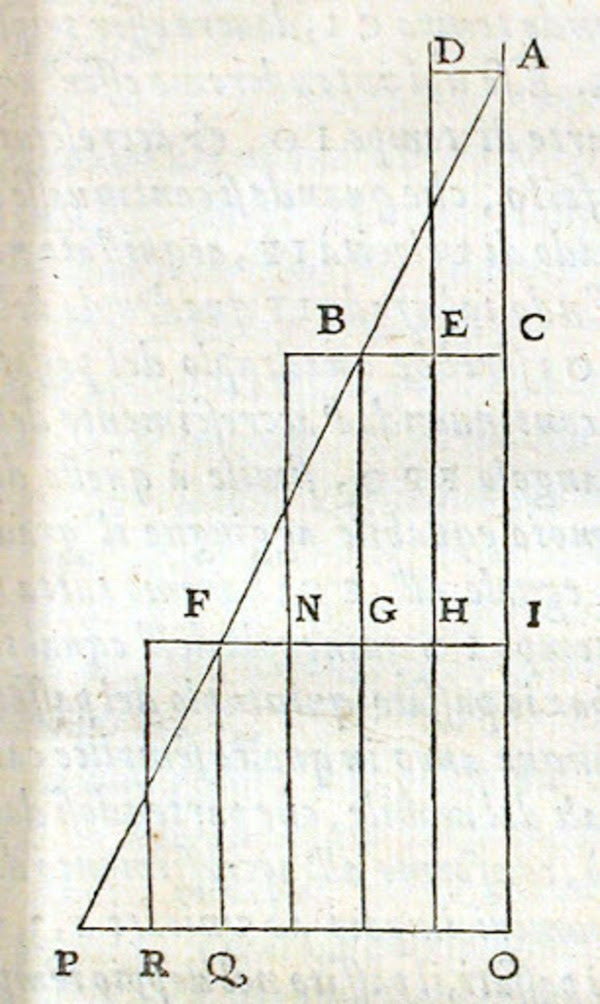
Figure 1. Galileo’s proof of the mean speed theorem which actually dates back more than two centuries to the Merton Calculators. Note how he approximates the area of the AOP triangle with lots of smaller rectangles such as ADEC. The text explains in more detail how this was discovered by the medieval Merton scholars.

Look at the triangle in the figure 1 (taken from Galileo). The vertical axis is time, while the horizontal axis is velocity. As time increases, so does the velocity, in proportion – this is what it means to be uniformly accelerating! The area of the triangle is the distance travelled (the base times the height divided by two). Why? The answer is as follows (and it might convince you that they understood the basics of calculus too, a fact that is perhaps not too surprising as this goes all the way back to Archimedes).

We need to represent the triangle as a stacked-up set of rectangles, which, as we make their height smaller and smaller, better and better approximate the hypothenuse of the triangle (I told you the Merton calculators understood the infinitesimals well before Newton or Leibnitz did; by the way, Archimedes calculated pi by doing the same thing with a circle instead of a triangle). When the rectangle is tiny, the speed during that tiny time remains almost the same. Therefore, the area of that rectangle (speed times time) is the tiny distance travelled. When you add up all the areas of the tiny rectangles you get the area of the big triangle (in the limit when the time in each rectangle goes to zero), therefore s = vf t/2, where vf is the final velocity.

(In passing, this method teaches us that the integral of t is t2/2, which is why the formula we learnt at school goes as s=at2/2).

Now, let me continue with the unbroken-chain-of-discovery theme. Quantum physics is often thought of as a radical departure from the classical ideas. Quantum systems behave like nothing we’ve ever seen before in the macroscopic classical world. However, while this is true conceptually (and experimentally!), if you look at the tweak that Heisenberg made in his original ground-breaking paper, it looks much smaller than that (though it took a hell of a lot of guts to do it and he was only 22-3 at the time).

Heisenberg didn’t change the classical laws of motion. No. For him, the distance travelled at a uniform speed was still equal to the initial distance plus the speed times time. Newton, and the medieval physicists before him, would have all been very pleased. However, he assumed that the distance and the velocity are not just mere numbers, but they become matrices (note that Heisenberg didn’t do that with time, which is the only outstanding variable remaining classical in all quantum laws of motion).

If you now work through two simple lines of math, you will see that if there was an uncertainty in the initial position of the particle, this uncertainty will now – in Heisenberg’s new mechanics – grow with time. It is something we technically call the “spreading of the wave-packet”. So, a small tweak in the math, leads to a large change in the physical behaviour (in classical physics, trajectories of particles do not broaden and spread out sidewise as the particle travels, but instead always remain just lines – a particle is always a point like object classically speaking).

To put this into perspective. If we drop an atom in the gravitational field (the quantum equivalent of Galileo’s leaning tower in Pisa work), the probability to detect the atom in a larger and larger number of places will increase with its fall! Good stuff that this does not happen with apples (it does, but to a tiny extent) as otherwise Newton would never have figured out what’s going on.

There are many other consequences to what Heisenberg did and we are still working it all out. Does quantum physics really apply to all objects and at all scales? We don’t know, but it seems to me that quantum physics is still an unfinished revolution. There are probably other things we need to quantize like, for instance, gravity. Or, which might well be related to gravity, time might need to be quantum instead of being mysteriously left in Heisenberg’s equations as a classical variable. It seems to me that time sitting in our quantum equations is much like an evolutionary equivalent of the human appendix.

But, more likely than not, there will be further tweaks taking us ultimately even beyond quantum physics. People have already been trying for a while (one immediately thinks of Penrose and twistors) but no one has succeeded just yet. We definitely feel (stupid?) like medieval Mertonian monks trying to grapple with some basic ideas regarding motion. We have had about a century of the new dark ages in physics (“dark” in the sense of no new laws of physics), during which quantum physics and relativity have simply passed all the tests we have been able to throw at them.

But I don’t think the current dark ages of physics will last long. We continue to be creative and our technology continues to improve. It is only a matter of time before the next “genetic mutation” happens to strike in physics, however – just like with the biological mutations – these events are really hard to predict in advance. But they invariably do happen sooner or later…