Do not enter if you do not understand geometry (or waves)

This statement (without “or waves”) was written on the entrance of Plato’s Academy (a.k.a. the first University in the World) in the Ancient Athens. He clearly thought that geometry was key to understanding the world. But more than that. He saw in it the rigor required from us when applying critical thinking to all ideas in philosophy. Geometry (as first formalised by Euclid, who lived about 100 years or so after Plato and was greatly influenced by him) works like this. We start with a few axioms, things that are self-evident about points and lines, and then proceed, by using the basic rules of logical inference, to deduce more and more complicated results (also known as theorems).

For instance, Euclid’s fifth axiom of geometry is this. Given a line, and a point that does not belong to it, there is only one other line that goes through that point and is parallel to the first line. Seems self-evident (WARNING: it is not – read ahead). From this and four other axioms, we could derive the whole of what we now call the Euclidian geometry. For instance, we could prove a theorem that the sum of all the angles in any triangle is 180 degrees (this is a highly non-self-evident statement and they don’t teach you in school how to prove it from Euclid’s axioms – though they really ought to).

And, from our own modern perspective, Plato was at least half right to emphasise geometry. One out of two of our theories needed to understand the whole universe – the General Theory of Relativity – is all about geometry. Einstein’s crowning achievement, the General Theory of Relativity equates gravity with the geometry of space and time. Gravity makes space and time curved (read: non-Euclidean; our universe actually violates the fifth axiom of Euclid’s!). So, gravity is all about geometry, but it is the geometry where given a line and a point outside of it, there are infinitely many other lines that can be drawn through that point and are all parallel to the first line (And, yes, the sum of angles in a triangle drawn in our universe actually adds up to more than 180!). There are many such non-Euclidean geometries due to Gauss, Bolyai, Lobachevski and so on…

But, to understand the rest of the universe we also need quantum physics. This is why I took the liberty of augmenting Plato’s dictum and added that we need to understand waves too and not just geometry. That’s because – and as I elaborated in an earlier blog – according to quantum physics, everything is a wave. All matter (and not just light itself) also behaves like waves.

And now we are ready to talk about a fascinating physics phenomenon that involves both waves and geometry, albeit all – at least as originally intended – from the world of classical physics. Enter Lord Kelvin.

One day, Kelvin was walking by the river Kelvin (hence his titular name) when he observed that ducks therein make the same wake in the water, more or less independently of their speed of motion. The angle of (what has since been called) Kelvin’s wake is about 39 degrees. And another amazing thing is that even the mass of the object moving through water does not really matter (you can have a look at the images of boats of different sizes in various revers and seas to convince yourself of the validity of Kelvin’s observation and the fact that they all generate the same wake).

This generality of the wake puzzled Kelvin initially, but he quickly came up with a rationale. I will try to reproduce his amazing argument here in as simple terms as possible.

First of all, moving objects in water generate waves. These waves interfere with one another and in some places they enhance each other, while in other places they cancel each other out. The wake is formed by two lines at which all the waves generated by moving ducks and boats actually add up and enhance each other. So much is clear and easy to understand. But why is this at 39 degrees?

Each wave is characterised by its frequency and its wavelength (or the wavenumber, k, which is the inverse wavelength). When a small volume of water is displaced by the moving duck it begins to oscillate. The key thing to realise is that the frequency of these oscillations is equal to the square root of the wavenumber times the gravitational acceleration g (=9.81 m/s^2). This is not difficult to prove using Newton’s laws, but for us the dimensional analysis will suffice (the dimensions of frequency are per second).

The phase velocity of the wave, which is defended as the ratio of the frequency and the wavenumber is now seen to be twice as big as the group velocity (which is the velocity at which the envelope of all the frequencies moves and is defined as the derivative of the frequency with respect to the wavenumber).

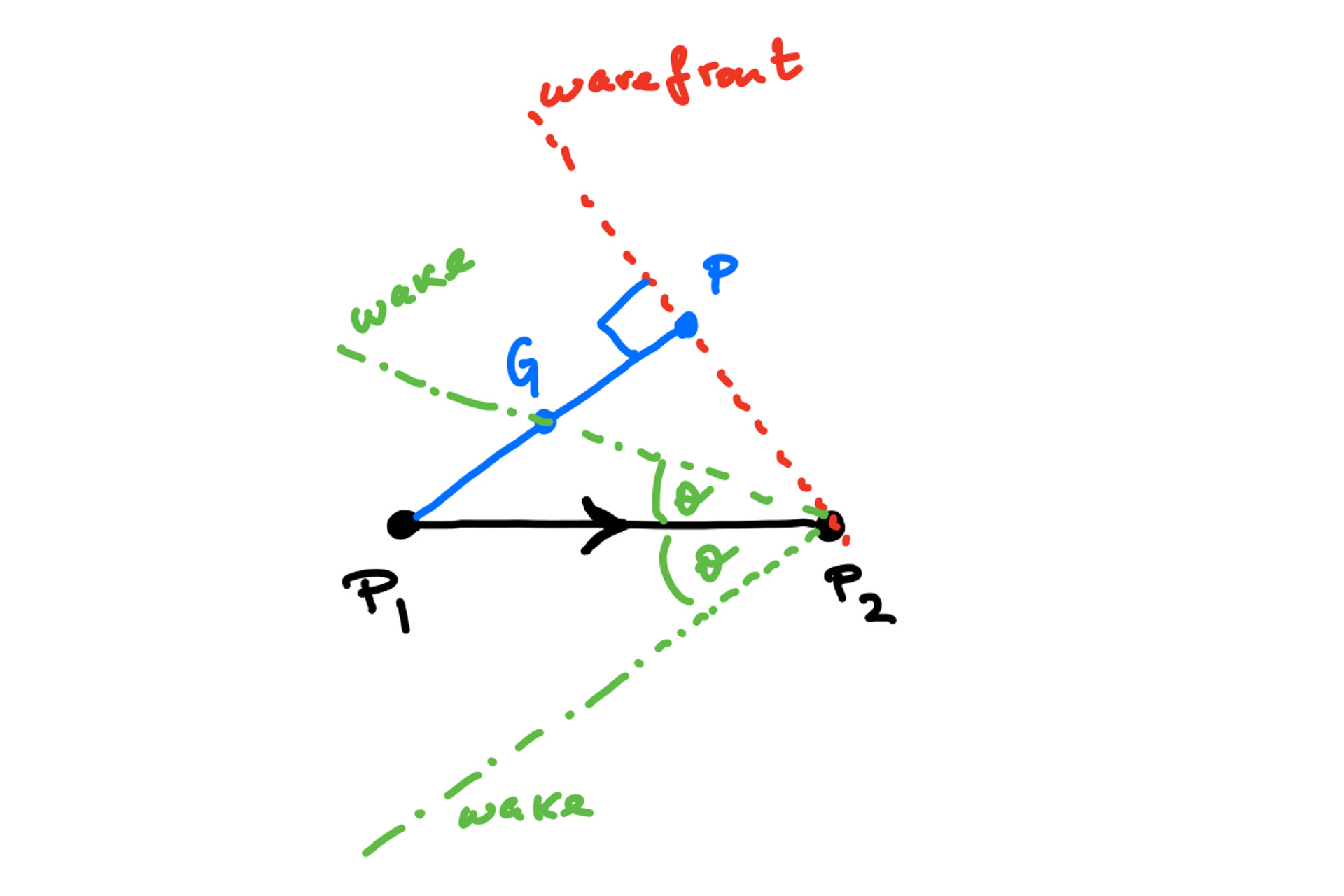
The line P1P2 represents the trajectory of motion of the duck. The red line is the wavefront and the green line is the wake. A brief outline of the calculation of the angle theta is explained in the text.

Once we know that the group velocity is half the phase velocity, we can use some simple geometry to do the rest (so simple that Plato and Euclid could have done it in their sleep). If you look at the diagram, the point P1 is the initial location of the duck, which then moves to the point P2. We can now draw the front of the waves at some angle to P1P2, which in the diagram is represented by the line P2P. The phase velocity is the line P1P which is perpendicular to the wavefront. Half of that perpendicular is at the point G and the segment P1G therefore represents the group velocity (since this is half of the phase velocity).

The group velocity is the velocity at which the bulk of the waves moves, so the line P2G is now the line of (half of) the wake. The angle theta, when we obtain its maximum allowed value, is therefore equal to half of the value of Kelvin’s wake. I won’t bother you here with the exact details of how to find this value, but – unless you want to have a go at it yourself – you can trust me that it involves about 3 lines of trigonometry.

Kelvin did the whole of this “back-of-an-envelope” calculation in his head while watching the ducks and then performed a more formal calculation when he returned to his home (which ultimately ended up as a paper published by the Royal Society).

This problem beautifully illustrates the counterintuitive nature of physical phenomena (here the independence of the speed and mass), but also the kind of reasoning including intuition and various different parts of mathematics (here both geometry and algebra) required for the ultimate understanding of even the simplest part of the physical world.

And, most importantly of all, there is the power of analogies. If, according to quantum physics, matter behaves like waves – and this is now beyond any experimental doubt, then we should be able to observe the Kelvin wake phenomena in quantum experiments with atoms. Take a condensate of about a billion atoms cooled to a very very low temperature, the so called Bose condensate, and it will collective behave very much like any other liquid. Introduce an impurity into this condensate, which could simply be another atom of different species, and move it about through the condensate (by, for instance, kicking it with a laser).

As the impurity atom moves though the condensate it should trace out a wake behind itself. This wake is made up of the waves of quantum probability, which, because the quantum waves are described by the same mathematics as the water waves, ought to lead to exactly the same angle of about 39 degrees.

Now, this is something that even Lord Kelvin could never have imagined possible.