From Micro to Macro

I’ve written a popular science book with this title, in which I explored various gaps between sciences which exist in our understanding of disparate phenomena at different levels of complexity. Gaps between physics and chemistry, chemistry and biology, biology and sociology, sociology and economics, frequently underpinned by various practical as well as – possibly – fundamental computational limitations. There are so many gaps that need to be bridged that we will never cease having pleasure of finding things out.

However, I would now like to emphasise (not the gaps but) the unity we have in some descriptions of the macro and micro phenomena. I’d like to tell you about two phenomena between which you’d expect there to be a big gap, but where, in fact, we have none. And it’s all to do with things ultimately being made up of quantum waves (as I have argued in some of my previous blogs) plus that some particles in those waves (bosons) like to bunch (they like to stick together when given a chance, a property I explored in my previous blog when I talked about indistinguishability).

The example of the unity I’d like to tell you about today is truly remarkable and connects astronomy with nuclear physics, spanning sizes that are separated by some 25 orders of magnitude (that’s a one followed by twenty-five zeroes!). The crux of this unity lies in the fact that we use one and the same method to measure diameters of stars and to measure diameters of atomic nuclei!

Let’s begin by explaining how we measure diameters of stars. There are various ways, but they all boil down to two things. One is to use the brightness of the star to estimate its distance from us (brightness, because of energy conservation, falls off with the square of the distance). The second is to measure the angular width of the star (the angle subtended from the Earth between the two far ends of the star). Once we know these two, the diameter of the star is equal to the distance multiplied by the angle.

It is the measurement of the angular width that relies on the interference of waves. The form of interference I have in mind here was first recognised by Hanbury-Brown and Twiss (two people, an astronomer and a mathematician).  They mounted, against quite a bit of criticism that their method wouldn’t work, two big satellite dishes on train tracks so that they could control the distance between them (on the order of 10s of meters or so). Then they measured what the intensity received from a particular star by one dish looks like when compared with the intensity received by the other dish. In particular, they were looking for a correlation: when one dish receives some photons from the star, does the other one receive more or less photons in comparison?

A simple quantum reasoning will tell us what to expect (as in the Figure below). Suppose a photon from one end of the start arrives at one detector and another photon from the other end of the star arrives at the other detector. But these photons are indistinguishable from one another. So the first photon could have ended up in the second detector and vice versa, criss-cross (as in the Figure below). In quantum physics, these two possibilities exist simultaneously in a superposition (and what a superposition it is, stretching as it does over hundreds of light years). We have to add them up in that way so that when we calculate the probabilities to get one photon in each detector this is the mod square of the two amplitudes.

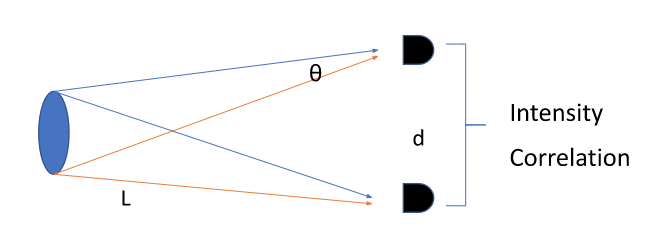
Figure. An object emitting a photon from two ends. Each detector could detect a photon in two different ways, blue paths and red paths which exist in a quantum superposition.

It is this probability that varies according to the distance between the detectors. And this variation is directly related to the angular width of the star. Actually, what I have just described is identical – mathematically speaking – to the interference pattern from two slits. I mean “identical”. Everything, as Feynman said, boils down to only one mystery in quantum physics, and it is that of the double slit experiment. One end of the star represents one slit, the other end of the star the other slit. It is a double slit of (literarily) cosmic proportions since the separation between the slits is millions of kilometres big and the distance to the detectors is many many light years.

And, now, at the other end of the spectrum, we have the atomic nucleus. It is one of the tinies objects in the universe. One side of the nucleus emits say a pion (a particle whose mass is between an electron and a proton – so called a meson, as it’s mass lies in-between) and the other side of the nucleus (a femtometer away) emits another pion. We then detect these two pions using two detectors (now separated by a few meters – not so different to the stellar interferometer!).  As we vary the distance between these detectors of pions, we gather the relevant information about the angular width of the nucleus, and thus (since we know the distance from the detectors to the nucleus) about the size of the nucleus.

So the same Hanbury-Brown Twiss idea allows us to measure the size of nuclei by just capitalising on the fact that some particles emitted by nuclei behave quantumly and are identical and indistinguishable bosons (pions in the case of nuclei), in other words they interfere by bunching.

As far as nuclear physics is concerned, the idea was realised by Goldhaber, Goldhaber, Lee, and Pais in 1960. It took sometime to understand that this is just the same as what Hanbury-Brown and Twiss proposed in 1954 for measuring stars. The reason it took time was partly because two particle interference effects were not properly understood until Glauber (mid-sixties) developed a full quantum optical treatment of such things.

But now, we know much more. What we call superposition and interference at the level of one particle becomes entanglement at the level of two particles or more. In fact, even a superposition of  a single particle can be interpreted as an entangled state if we use the formalism of second quantisation where particles are just excitations of modes (something I could explore in my next blog). When we have more particles, even entanglement could be entangled (oh, yes, this is amazing and also something I could talk about next time, if I decide to explore hierarchies of entanglements), but this is really just an even more complicated form of the one and same quantum superposition. The state of everything in the universe is that of entangled entanglements and people like me find it intellectually very pleasing that the universe uses the same basic quantum tricks at both the smallest and the largest of scales.