Spacetime, Causality and the Quantum

The whole seemingly paradoxical nature of quantum physics (by paradoxical I simply mean that it does not conform to the rules of the ordinary classical logic) stems from the linearity of quantum operations. Namely, if we can execute two different unitary transformations on a given system, then we can also execute them in a conditional way by controlling which unitary is applied depending on the value of an additional qubit. Specifically, if the additional qubit is in state zero, we apply one of the two unitaries, whereas if the qubit is in the state one, we apply the other unitary. The case of greatest interest to us is when the qubit is initially in the superposition of the states zero and one.

This is an overall unitary transformation and it, of course, leads to entanglement between the qubit and the system undergoing conditionally the two unitary transformations. This transformation is the key element in the Schrödinger cat thought experiment as well as being at the root of quantum computation. One could say without much exaggeration that a controlled unitary operation is at the heart of every genuine quantum experiment (which ultimately usually involves the final measurement of the qubit in the zero plus/minus one basis, after the controlled unitary has been applied).

Despite almost hundred years of quantum physics, however, we still find some consequences of the above transformation surprising. For instance, relativistic Lorentz transformations are represented by unitaries in quantum theory. This is natural as the amplitude in quantum physics ought to be a relativistically invariant entity (strictly speaking it is only the probability that needs to stay invariant, but this is not relevant for the present discussion).

Now, imagine that we prepare a spatial superposition of a particle and then apply a Lorentz boost only if the particle is in one of the two locations (and do nothing if the particle is in the other location). Now we have a superposition of two different velocities of one and the same particle. The qubit here is the spatial location of the particle, which provides the control.

According to the Special Theory of Relativity, the clock of the particle in the moving branch of the superposition runs slower than in the branch where the particle is stationary. Imagine finally that we interfere these two branches. It would result in one particle localized in space (this is what we mean by ‘interfere’), but in a superposition of two different times (i.e. a superposition of a younger and older versions of one and the same particle). Quantumly this entity is in a superposition of two proper times.
The experimenter has their own time in which the experiment is conducted and this time is presumably the same as the faster of the times of the particle (assuming that the experimenter was stationary with respect to the particle that was not moving). There is no contradiction here, since times could indeed be different for different observers.

As we said, if two things are possible classically (such as moving at two different speeds) then in a quantum experiment we can always prepare their superposition. And we can make superpositions of superpositions and so on, ad infinitum.

Suppose now that we have two spacelike events, which are events that cannot causally affect one another as they are separated by a distance larger than the time it takes light to travel between them. For instance, a church bell striking 1pm in Paris, and in Stockholm (they are in the same time zone and I am assuming that the churches are perfectly synchronized) are events that are spacelike because it takes light about 6 milliseconds to travel between the two places.

This means that there are observers which will think of these events as being at the same time (anyone being stationary with respect to the churches such as someone living in Paris), but there will be observers which will think of one of them being before the other and vice versa (depending on the way they happen to be moving)! This is what relativity tells us.

When you mix in quantum physics, you can actually prepare a superposition of these, namely you could have a branch in which the bell strikes one in Paris first and then in Stockholm and another branch in which the observer perceives these two events in the opposite order. This is something that is – in my view mistakenly – called a state of “indefinite causal orders”. It is more proper to say that each element of the superposition has a causal order, but an observer outside of the superposition (like the cat in Schrödinger’s experiment before the poison is released) certainly has to acknowledge the superposition and cannot say more than that.

The above example is, incidentally, also a superposition of different “arrows of time”. One observer will say that as time flows (if this is what time does?), it first encounters the chime of the Parisian church followed by the Stockholm one, while for the other observer the time would flow “backwards” in the sense that the chime of the Stockholm church would happen earlier than the Parisian one. All this is a straightforward consequence of quantum physics when combined with relativity.

One might get the impression that anything is possible in this world of quantum relativity. However, the exact opposite is closer to reality. The laws of quantum physics and relativity are very prohibitive and stringent. Light always travels at the same speed for all observers and no information can travel faster than it. All observers have got to agree on the laws of physics; if one observer says that a photon entered one of your eyes (say the left one) then all other observers (no matter how they are travelling) have got to agree (this is why we insisted on the Lorentz transformations being unitary meaning that they don’t change probabilities for different observers).

I want to close with something I’ve always found surprising, but it does illustrate the subtle “tightness” of the laws of physics. Add to the above two churches another one, this time in Rome. They all strike one at the same time for someone stationary with respect to them. Now, let’s discuss the orders for other observers. You’d probably say, all must be possible. I will use the notation RPS to mean that the observer hears first Rome, then Paris, then Stockholm bell. Then we have six possible permutations (RPS, RSP, PRS, PSR, SPR, SRP) each corresponding to a different arrow of time.

The interesting thing is this. Not all permutations are possible according to relativity. For simplicity, I am assuming one spatial dimension, in the sense that the churches lie on the same line (my geography has never been strong), but the result is true for 4 and more events in the 3 dimensional spatial world (for general statements see for example the arxiv paper by Mark I. Heiligman). There is a very simple reason for excluding all possible permutations of events. If there exists an observer that sees RPS, and another one that sees RSP, then for an observer to see PRS they would have to travel faster than the speed of light. And this is not allowed according to relativity (see the diagram below).

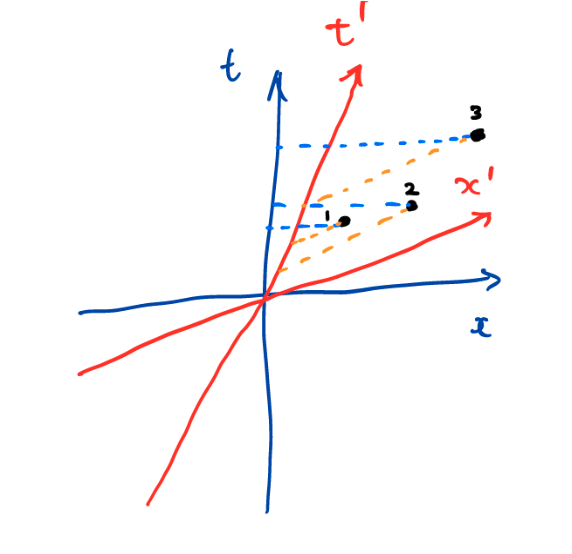
Image (c) Vlatko Vedral

Note also that this automatically constrains quantum physics (laws of physics always work together this way even if they originate independently of one another as did relativity and quantum physics). Namely, we cannot prepare a superposition of these observers either. The story would of course be different if the events were timelike since then all observers would have to see them in the same order. They are then causally linked in a unique order for all observers (such as “you pressing the remote control” being one event, followed by the “TV switching on” as another event – no observer can see this in reverse as far as relativity is concerned).

This also says nothing prohibitive about preparing superposition of applying three different unitaries in six different orders (123, 132, 213, 231, 312 and 321). This is, of course, possible and is – in fact – a routine part of any more complex quantum computation (you could program the existing IBM cloud quantum computer to perform this operation). The orders are simply well defined in each branch of the superposition, but not for an outside observer who only has access to the superposition itself. Nothing out of the ordinary as far as quantum physics.

Quantum physics is magic, but not in the sense that the impossible becomes possible. Quantum physics is magic, to paraphrase Arthur C. Clarke, because it permits an exponentially more advanced form of information processing technology than anything allowed by the laws of classical physics. But it contains no paradoxes or inconsistencies, only things that might be counterintuitive to the uninitiated.